Counting occurrences of digits(0-9) in a set of numbers
Last Friday, I had a conversation with a data scientist and he posed this programming question to me: “Count the number of occurrences of each of the digits 0-9 in a given set of numbers”. At first, the problem sounds simple, but given the multiple ways with which it can be solved, makes it very very interesting and a good learning experience.
I am sure there are many methods to solving this problem, but here’s my 2 cents.
Approach 1 : Convert the numbers to strings
1.A : Using ‘str_count’ function
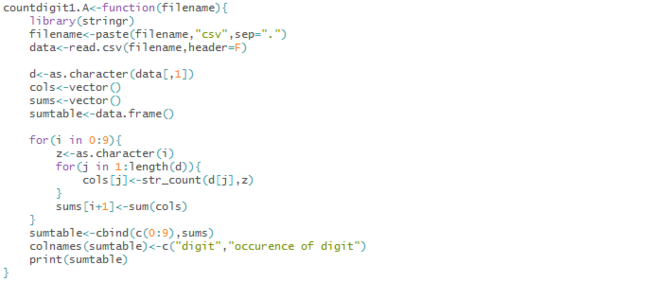
View above code as text
1.B : Using ‘gsub’ and ‘nchar’ functions

View above code as text
1.C : Using ‘stri_count_fixed’ function
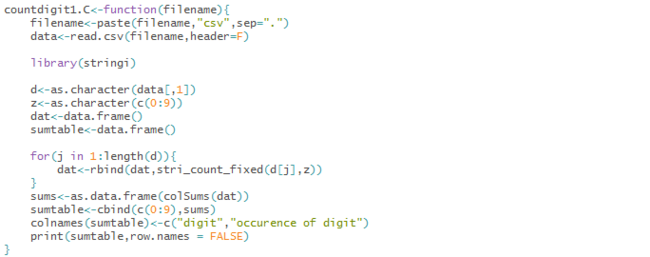
View above code as text
Approach 2 : Leaving the numbers as numeric
Moving right along, let’s do a performance evaluation of each of these methods. Here’s a snippet code that can help us calculate time taken for the data to process through the function and throw out an output:
For the performance test, we will use 3 datasets containing random numbers between 0 and 10000 with lengths(number of rows) of 1000, 10000 and 100000 respectively, and run them through each of the above three functions of the first approach to compare their performance against each other over increasing data set size.
Below table, summarizes the results of the test. Note that the columns represent the different methods, while the rows represent the increasing data set size.
As seen from the table, method B is the fastest, while method C is the slowest.
Sanket


